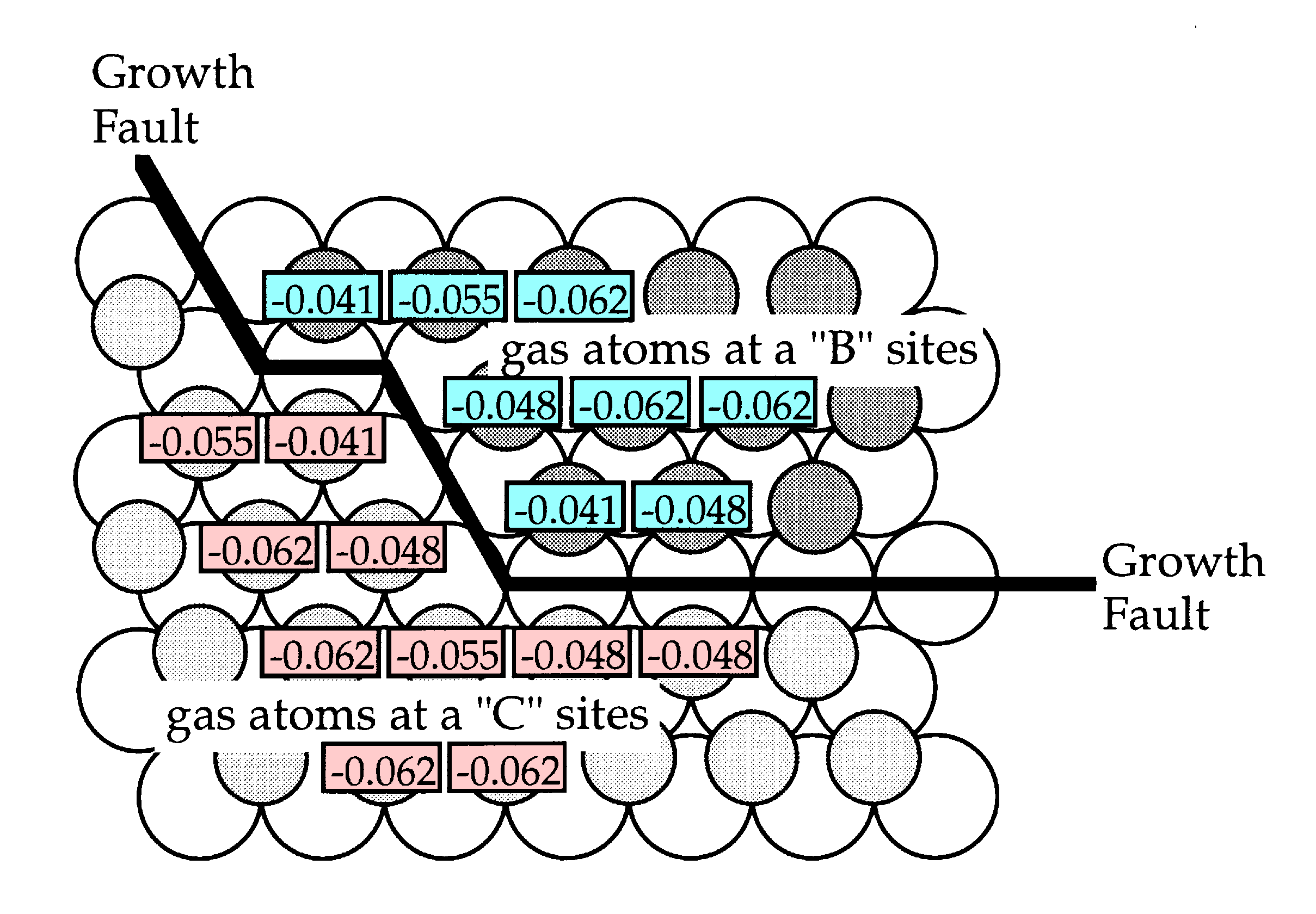
Consider the specific interface between two islands depicted below. Above each atom is its calculated attachment energy. It is clear that interface sites have lower attachment energies compared to sites which have a full complement of neighbours. This has two implications. First, interface atoms have a higher probability of evaporating. Second, atoms that are incident on a interface site are less likely to become attached. Consequently, the evolution of the atomic distribution is more active at interfaces.

However, the situation is complicated by the fact that some interface sites have substantially lower attachment energies than others. Thus the more highly convoluted an interface, the more quickly it becomes modified through the evaporation attachment process. Furthermore, not only is there an energetic imperative for this to occur, there can also be a crystallographic hinderence effect. This can most easily be understood if we consider a straight (1,0,-1,0) interface.
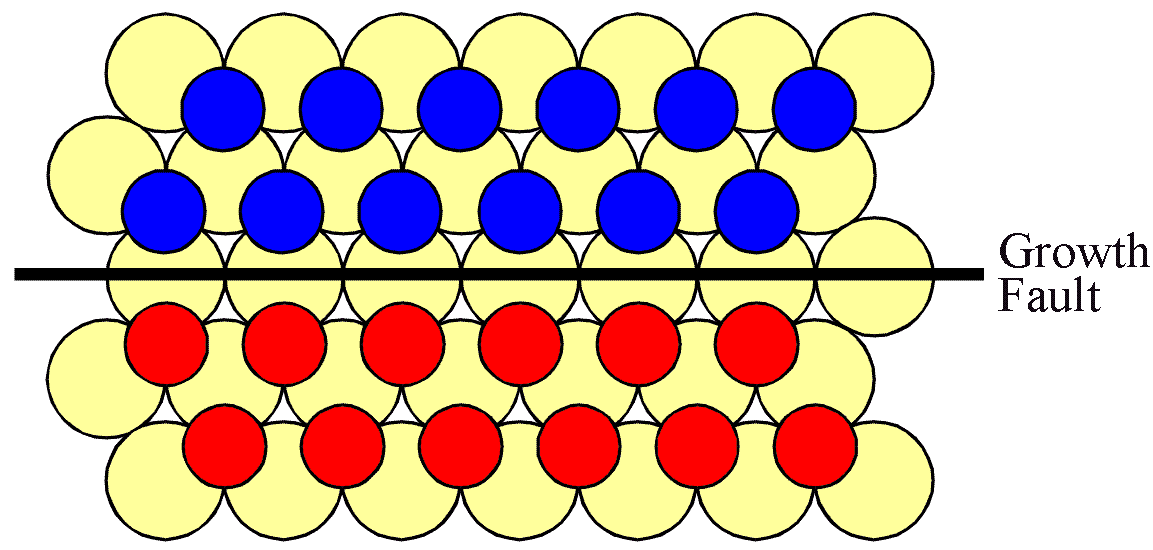
For the interface to progress upwards, expanding the "C" island, a "B" atom must be lost. This is shown in the next figure.
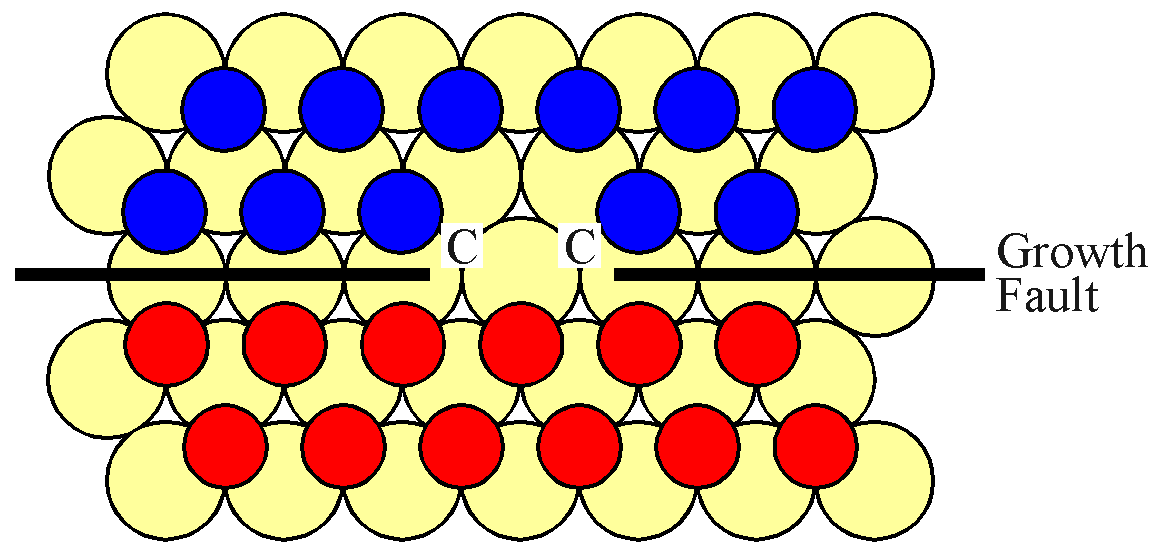
However, both of the potential "A" sites are hindered by "B" type atoms. Thus a second "B" atom must evaporate, adjacent to the first site. This situation is shown in the next figure.
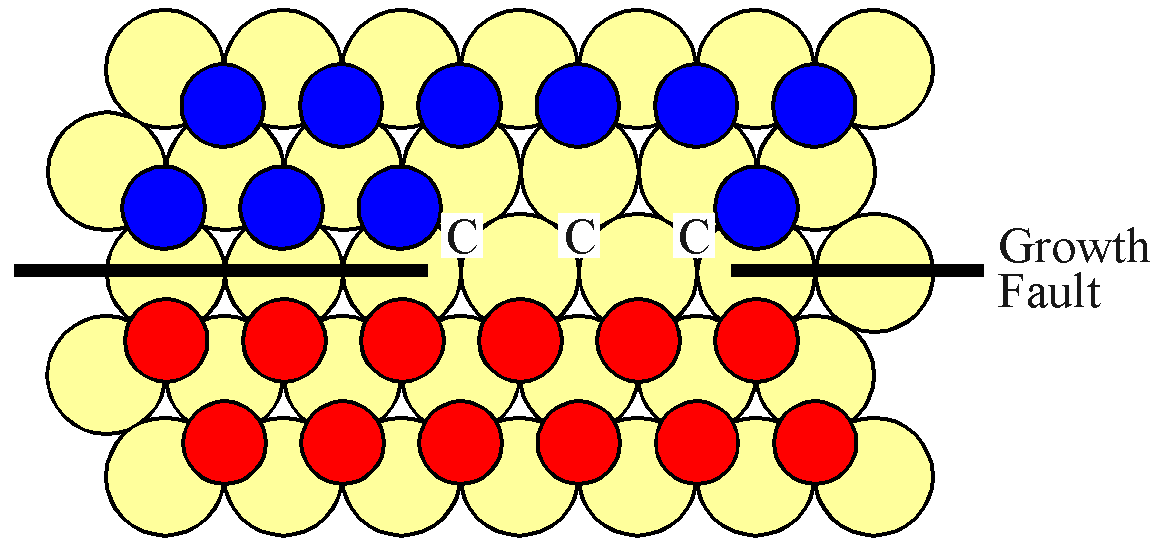
It is now possible for a single "C" type atom to attach itself to the surface, effectively expanding the "C" island as shown. Of course, the probability that two atoms are lost adjacent to each other is correspondingly small. Furthermore, this "C" type atom has only two neighbouring "C" type atoms which means that its attachment energy is lower than if a "B" type atom were to reattach itself. Thus the expansion of a straight boundary is subject to energetic and probabalistic barriers.
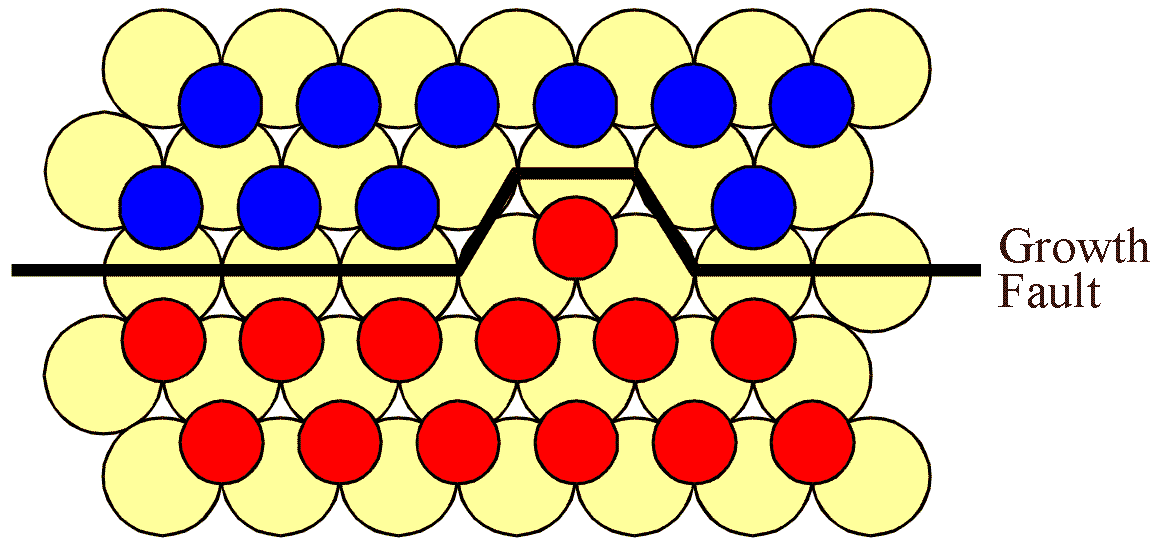
By running the argument the opposite way round it is possible to see that these type of convoluted structures will tend to be removed as the simulation progresses. Indeed, by applying this analysis to other situations, one can conclude that boundaries should straighten on an atomistic level. Of course, this is a well known experimental observation which is usually discussed in terms of surface tension.
At temperatures close to the maximum for island growth, the lower attachment energies of interface ions can have the effect of forming regions, adjacent to interfaces which are denuded of ions. These show up on the simulations as dark areas. However these are usually small and hard to see.
One of the potential problems that has become apparent during the progress of this study concerns the reliability of predicted rates of island growth. Here we calculate an energetic advantage of atoms in the interior of islands over atoms at an interface region of between 10 - 50 %. The simulation is then run for 2,000 time steps which corresponds to approximately a microsecond. If the relative attachment energies were slightly different, the predicted temperatures at which the maximum in island growth occurs could be quite different. This is a general problem which should be given more attention. However, for many systems, experimental data may be available in which case, the energies could be learnt by running the simulation and matching this simple parameter.
In this model, each CA cell contains two sites of which only one may be occupied. This is fixed. Although we are able to simulate a greater number of atoms (~105), over a far longer total time interval (~10-6 s) than any previous MD type simulation, for the modelling of a three dimensional atomic microstructure, we are still very limited. For example, a typical grain in a conventional microstructure would be at least ~0.1 micrometres across. This would encompass ~5x107 atoms. Clearly we would wish to include more than one grain in any simulation! In addition, a typical heat treatment would last for at least 103 seconds. The approach to predicting real three dimensional microstructural evolution will have to be fundamentally different. The most obvious modification would be to include multiple atomic sites in a single CA cell. Nevertheless, the properties of atoms in the CA cell could and probably would have to be learnt from a combination of smaller scale CA or even MD simulations. As such, we envisage a hierarchy of models which culminate in a full blown real scale simulation. In this regard, the scales of the present simulations are important.
In the short term, it would be very useful to run energy minimisation atomistic simulations of atoms in a variety of situations and formulate a more complete look-up table of attachment energies thereby formally completing the atomistic to CA loop.
Certainly a number of tools would be useful in providing analysis of the simulations. The first would be a way of reporting island size. This would allow us to quantify the extent of the grain growth over a given simulation time and grain growth rates as a function of temperature and pressure.
There are a number of additional topics which the present code should be used to address. The first is to introduce another atom type. A particularly interesting example would be xenon which due to its greater mass and higher polarizability would stick to the surface and attract neighbouring Ar or Ne atoms strongly. It is envisaged that xenon would then act as an island growth inhibitor, effectively pinning convoluted structures. Again this is not a technologically important example but it would expand our assessment of what this type of model can simulate successfully.
In these simulations, we start with an empty surface. As an alternative, we could begin with an idealised boundary and investigate how this evolves. For example, to what extent will a perfect straight (1,0,-1,0) boundary become convoluted over a period of time at a given temperature? Certainly it should, due to entropic effects, but to what extent is less clear.
It would also be possible to investigate the specific rate of shrinkage of a boundary as a function of island radius by initiating a simulation with a single circular island of specified radius.
It would be a simple matter to extend the present code to include diffusion since in this 2D context, this corresponds to activated hops into vacant sites. The activation energy can easily be calculated using energy minimisation atomistic simulation. Within islands, if migration is mediated by a single vacant site, this corresponds to "B" to "B" or "C" to "C" jumps. However, at a boundary between "B" and "C" islands, there is the possibility for "B" to "C" or "C" to "B" jumps which would have a lower activation energy. Interior "B" to "C" to "B" double jumps are also possible if there are two adjacent vacant sites. It is important to bare in mind that diffusion effects have the potential to dominate the kinetics of island growth.
In the present code, the crystallographic orientations of surface islands are defined by the substrate coupled with the matched sizes of the Ne and Ar atoms. This gives rise to a very limited number of boundary orientations. In particular, it means that straight boundaries formed when islands of different orientation meet cannot be formed (i.e. boundaries that are not simple mirror images of each other). However, the manner in which such boundaries develop is of great potential importance, because matched sized systems are not the norm. One way forward in this regard is to use a coincidence lattice site theory approach where the boundary is composed of a periodically repeating set of local environment CA cells. Each CA cell would correspond to a set of atoms which would have evolution or migration properties which were predetermined using MD or quasiharmonic modelling techniques. For visualization, each CA cell would have as an attribute, a shape which was a function of the nearest neighbour relationships of the component atoms.
Another obvious limitation of the present code is that it can only simulate a 2D surface. However, it may not be too onerous a task to extend the code to 3D if the aim is to model a deposition process. The reason is that the principle factors in the kinetics of surface deposition, and hence thin layer morphologies are surface processes. Thus as a surface is covered with new material, on the time scale of surface deposition, atoms now beneath the surface may be regarded as inactive as far as the kinetics of the surface evolution is concerned. Of course, they will continue to influence the surface atoms through the attachment energy. The obvious way in which this could be achieved in terms of CA modelling is to assign each CA cell a height and a corresponding register of atoms. Thus as the simulation proceeds and the number of atoms in the system increases, the code does not become memory limited and remains efficient.
Finally, the code could be modified to model the deposition of molecular species. This would be particularly useful in modelling catalytic processes where molecules such as CO poison surfaces. The essential modification would be to associate each CA cell site with an orientation aspect. Also, each cell may have a number of sites each of which could potentially accommodate a molecule, or part of a molecule. In this way, a variety of molecular sizes could be attached in adjacent cells. This would have benefits for the modelling of deposition processes where atoms and molecules in the incident beam can interact with each other forming clusters in advance of deposition. Under such circumstances, momentum transfer effects may become important. Although this is an area in which there is little knowledge at present, it will be the focus of a forthcoming project which will employ MD techniques to study low energy atomic bombardment of ceramic surfaces (Grimes and Sickafus ICSTM from October 1997).
One aspect of the overall debate that we have not been able to consider thoroughly enough is the extent to which the details of the local atomic structure influence the final microstructure. Certainly we would expect the kinetics to be strongly controlled and hence the grain sizes but whether the type of microstructure (i.e. equiaxed , columnar etc.) is so critically affected is not so clear. Traditionally microstructural evolution models have been based on surface tension forces and diffusional mass transfer. Both of these could be translated into CA rule sets. For example, the local curvature of a boundary which crosses a CA cell is a parameter which would be affected by the curvature of adjacent cells and would control mass transport across the boundary within the cell. However, mass transport is highly anisotropic because of the details of the local crystal structure. Thus it is hard to envisage how neglecting the effects of crystallography can result in anything other than an empirically modified isotropic model.
Nevertheless, we cannot remain constrained to atomistic scale CA cells and expect to further improve computational efficiency to the extent necessary to undertake three dimensional microstructural modelling over long time scales. Thus it would seem inevitable that rather then associate specific crystallographic positions with a CA cell, it is more tractable to associate a crystallographic orientation and thereby introduce anisotropy into the rule set. Thus, the probability for mass transport, evaporation etc. would depend on boundary curvature and crystallographic orientation. Naturally this rule set would have to be compiled beforehand. Since experimental data will usually not be available, it will have to be derived using other modelling techniques. However, the reason for embarking on the present AR-CA study was partly because this type of data is computationally expensive to derive using MD or energy minimisation techniques. Thus the most likely solution would seem to be a hierarchy of methods starting with MD or energy minimisation, predicting rules for use in a AR-CA code which in turn provides the macroscopic rule set.
The possibility of any favourable comparisons with microstructures in bulk solids would seem to be unlikely and of dubious validity at this stage. Nevertheless, the following figure is presented for the copper-phosphorus eutectic, an immiscible binary system.

(Micrograph taken from "Materials Science" by Anderson, Leaver, Rawlings & Alexander)
Our present model assumes no attractive interaction between "B" type and "C" type islands but only a very short range repulsion. In this respect, the two types of gas atom islands are acting as if they were immiscible, although the immiscibility has a crystallographic rather than chemical origin. Furthermore, transport of atoms in this two dimensional system are via evaporation into the gas phase rather than by surface or solid state diffusion as might be expected in the three dimensional metallic system. Nevertheless, it may be that the basic model for a binary immiscibile system presented here is all that is necessary for this type of microstructure to be formed. The method of material transport may be largely responsible for the kinetics of growth rather than for the gross microstructural features. Therefore, although the authors wish to stress that considerably more work is necessary before firm conclusions can be drawn, (in particular diffusion rules must be introduced into the model) these results are certainly encouraging.
 our address: Department of Materials, Imperial College,Prince Consort Rd, London SW7 2BP, UK
our phone: 0171-594-6802, 0171-594-6730 (Robin's)
our address: Department of Materials, Imperial College,Prince Consort Rd, London SW7 2BP, UK
our phone: 0171-594-6802, 0171-594-6730 (Robin's)