Of course, the system we will consider here is rather specific and not itself of great technological importance. However, to the authors knowledge, this is the first time that atomistic simulation data has been used as the basis for CA rules. As such, this study presents a powerful new methodology for bridging between atomistic and microstructural scale simulations.
Since this is an atomic scale problem, it is necessary to account explicitly for the interaction between a gas atom and the calcium surface and between a gas atom and its neighbouring gas atoms (inter gas atom interactions). Interatomic potentials were therefore derived which describe the interaction energy between atomic species as a function of interatomic separation (these will be described in detail below). Thus, once we know the position of a gas atom on the surface and its number of neighbouring gas atoms, it is straightforward to determine its stability. In the approach used here, these energies are translated into local rules for the CA engine.
The starting point for all the simulations described here is a bare metal surface. The gas atom layer is deposited onto the surface, from the gas phase, as a flux whose magnitude can be varied. Gas atoms may also desorb from the surface. The surface therefore evolves via a combination of adsorption and desorption processes both of which are temperature dependent via the CA rules.
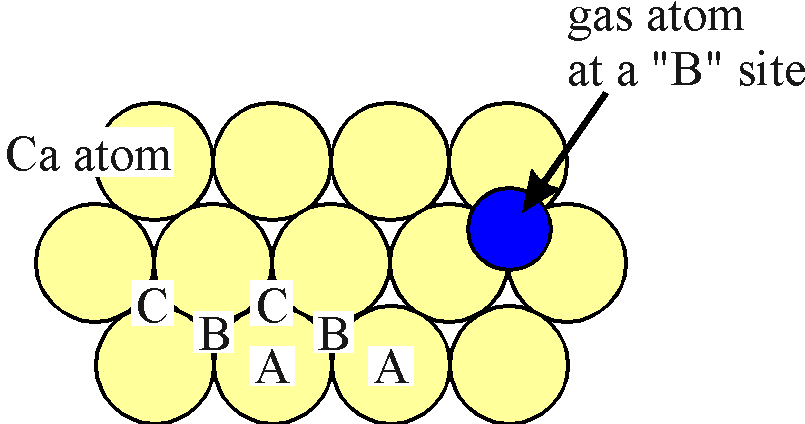
Clearly it is essential to understand the physical basis of the CA rules. Thus in the next section we will consider the (111) surface structure and the positions of the gas atoms in detail.

If we examine the (111) surface more closely it is clear that the distance between an interstitial "B" site and a nearest neighbouring "C" site is rather short. Indeed the gas atom in the figure above (which represents neon in scale to calcium) overlaps considerably onto the "C" site. As such, if a gas atom resides in a "B" site, it is not possible for a second gas atom to occupy an nearest neighbour "C" site due to steric hindrance. It is important to realise that this is true only because of the specific matching of the size of the Ca (111) surface to the sizes of the Ar and Ne ions.
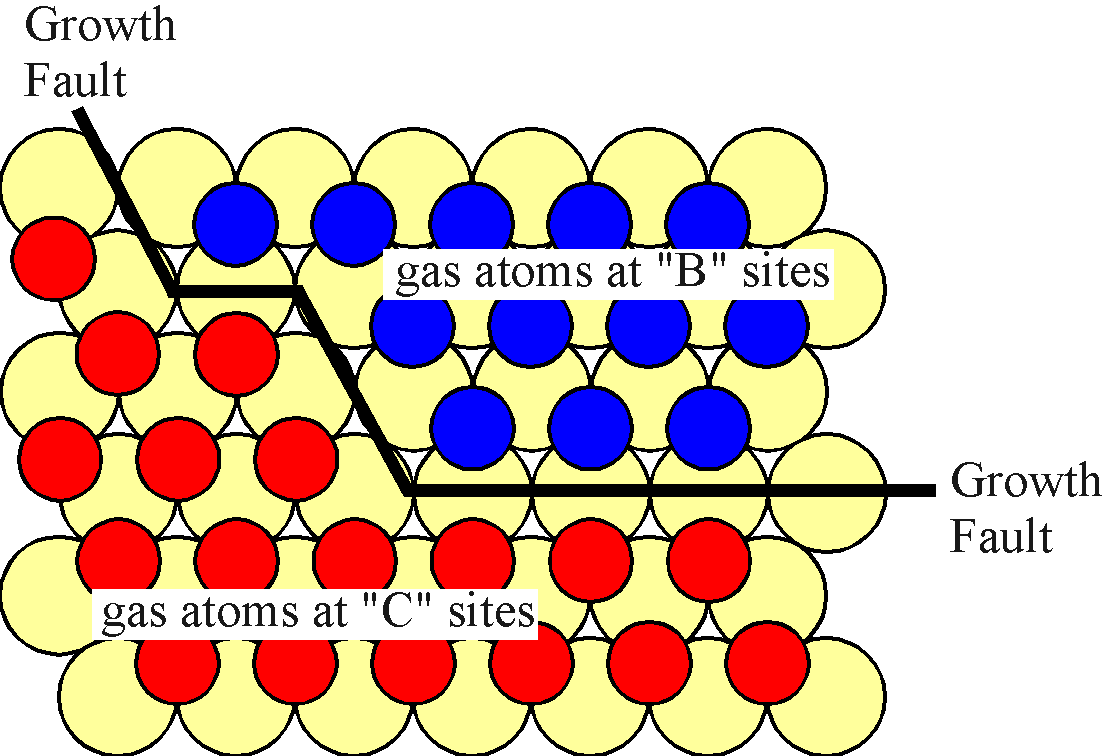
Let us now consider the evolution of the gas atom layer as follows. When the first few gas atoms impinge on the surface, they may reside in either A or B sites. As more atoms collect, patches or islands of B-type and C-type atoms form. In the diagram below, it is clear that the distance between two nearest neighbour B-type gas atoms is the same as between two C-type gas atoms. However, the distance between allowed, none hindered B-type and C-type atoms is greater. This results in an area of surface with a lower density of gas atoms which will be termed a growth fault. In three dimensions, it would give rise to a stacking fault. This is important to the stability of a gas atom on the surface since when gas atoms interact over a longer distance, their interaction energy is lower. Indeed, this is the driving force which results in the formation and growth of islands of gas atoms which are occupying only one type of site.
where A and B are constants specific to atoms i and j. For each potential type, the constant "B" corresponds to the van der Waals interaction and can be determined from the polarisabilities of the interacting ions via the Slater Kirkwood formulae (see Fowler et al. Mol. Phys., 56, 83, (1985)). For the inert gases, the "A" constants were determined by ensuring that the appropriate potential reproduced the lattice parameter of the inert gas lattice (note that both neon and argon exhibit FCC latticies). For the inert gas - metal interaction, the "A" parameter was chosen so that the potential has a minimum corresponding to rij = gas radius + metal radius.
| Potential type | A (eVAng12) | B (eVAng6) |
|---|---|---|
| Ca - Ne | 12276.6 | 12.54 |
| Ca - Ar | 64447.4 | 40.90 |
| Ne - Ne | 1953.89 | 4.14 |
| Ar - Ar | 53845.3 | 40.90 |
Once the parameters have been determined, it is possible to calculate the interaction energies, which define the stability of an atom at a specific site on the surface. Usually with atomistic simulation, a calculation would be carried out during which all atoms would be allowed to relax to zero force. In ionic systems, where long range Coulomb forces operate, this is critical. However, in this highly symmetric system, where energies are described by short range van der Waals interactions, a more simple approach is justifiable. First, the interaction of a gas atom with the substrate is given by three times the energy of interaction of a gas atom with a single calcium atom at; rij = gas radius + metal radius. Second, the interaction energies between nearest neighbour "B" gas atoms is given by the value of the potential at; rij = Ca - Ca nearest neighbour distance = twice the Ca metal ion radius. Remember, the separation of the gas atoms is defined by the substrate. The same is true for interactions between nearest neighbour "C" gas atoms. The total interaction between a gas atom and its nearest neighbours depends on the number of nearest neighbours. This is, of course, a key feature of the model.
A further simplification is made to describe the interactions between "B" site gas atoms and nearest allowed "C" site gas atoms: they are assumed to be zero. Although this may seem a somewhat draconian assumption, the increase in the gas - gas distance in the (2,-1,-1,0) direction (hexagonal coordinate system) over the nearest "B" - "B" is 1.5366 which implies a reduction in the gas - gas interaction by a factor of 13. The reduction in interaction in the (0,1,-1,0) direction is somewhat less, a factor of 2.2. Given this, it would be interesting, in future work, to account for the "B" - "C" interaction in the (0,1,-1,0) direction which may lead to some anisotropic growth effects.
Given the above rules, it is simple to calculate the energy that a gas atom would experience if it were to occupy a specific surface site. This will be known as the attachment energy, Ea. Note that because of the way that the interaction potentials are defined, negative attachment energies are favourable.
This leaves us with the problem of relating the attachment energy to;
This will be the subject of the next two sections.
The fraction of incoming atoms that stick to the surface depends on the substrate's ability to dissipate a sufficient proportion of the kinetic energy of a colliding atom for the atom to become trapped in the potential well. Thus, we make the assumption that any atom with kinetic energy less than Ea will stick. Thus;
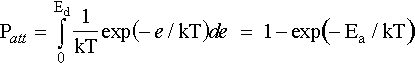
where the desorption rate, Rd, is given by;
where T is temperature in Kelvin, k is Boltzmann's constant, gd is a geometric factor (which we take to be unity in this case) and fo is the attempt frequency. Thus, the total number of atoms which desorbe over a single time step, st is;
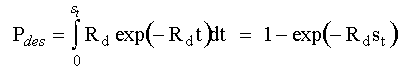
The attempt frequency is, to a good approximation, equivalent to the vibrational frequency of the gas atom on the surface. This can be determined from the interatomic potentials. Here the energy of each gas atom was determined as a function of its distance perpendicular to the surface, assuming a full compliment of neighbouring gas atoms (i.e. a symmetric site). Harmonic functions were then fitted to each energy profile to yield the force constants. The characteristic frequencies were then determined from the force constants: these were 4.45x1010 s-1 for Ar and 4.59x10-1 s-1 for Ne.
If the attempt frequency is not known, it can be assumed to be equal to the reciprocal of the time step, in which case, the desorption probability simplifies to;
which is approximately equal to exp(-Ea/kT) when the value of Ea/kT is small. However, if this approximation is made, we cannot relate the flux to any real time scale and the only simulations that are definitive are those that run to equilibrium.

This is an atomistic model which naturally lends itself to the implementation of the type of relationship discussed above. The flux used here was 15%, that is, the number of gas atoms which were allowed to interact with the surface corresponded to 15% of the total number of surface sites (B and C). It is important to realise that some of these atoms could attempt to interact with the same surface site. In this case, only one atom is allowed to be successful. This way of implementing the flux is realistic since gas atoms interact with the surface continuously rather than in the step wise discrete manner of CA. However, if two atoms attempt to simultaneously occupy nearest neighbour sites, none are allowed to be successful. This is not physically realistic for the long CA time steps used, but it is computationally much simpler than any alternative choice algorithm yet discovered.
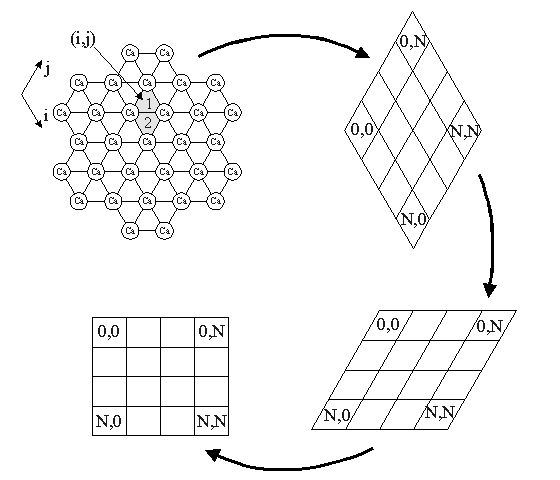
Once the flux value is chosen, for a given box size, this defines the number of gas atoms, each of which are assigned a random number from 1 to the total number of surface sites. Integer division by 2 is then carried out to yield an integer and a remainder. If the remainder is zero, the atoms will strike a "B" site, if it is one, it will strike a "C" site. The integer value assigns the atom to a surface cell which contains a "B" site and a "C" site. The number of surface cells is, of course, half the number of surface sites.
It would be a great advantage to be able to relate the flux to the pressure of the gas above the surface. In this case, we can define the flux in terms of the number of atoms striking a surface area in unit time and relate this to the velocity of an ideal gas.
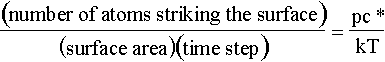
where p is the partial pressure of the gas and c* is the mean velocity of the incoming atoms. Then,
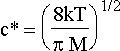
so that the flux can be related to the pressure by
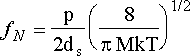
where ds is the surface density of absorption sites and M is the mass of the absorbing species.
The first rule assigns to each atom incident on to the surface a random number from one to the total number of surface sites.
This number then undergoes integer division by two.
The second rule uses the value of the remainder from the integer division. If the remainder is zero, the atom is incident on to a "B" site, if the remainder is one, the atom is incident on to a "C" site.
The third rule uses the integer value from the integer division. The integer value assigns the atom to a particular cell on the surface.
The combination of a surface cell and the assignment of "B" or "C" site yields a unique interstitial site.
The second rule concerns the hinderence that an occupied "C" site has to "B" site occupation and vice versa. When the flux directs a gas atom to a "B" interstitial site that has a gas atom at a nearest neighbour "C" site, the gas atom will not become attached to the surface. There is an equivalent hinderence rule for gas atoms directed to a "C" site.
 our address: Department of Materials, Imperial College,Prince Consort Rd, London SW7 2BP, UK
our phone: 0171-594-6802, 0171-594-6730 (Robin's)
our address: Department of Materials, Imperial College,Prince Consort Rd, London SW7 2BP, UK
our phone: 0171-594-6802, 0171-594-6730 (Robin's)